transform属性的数学原理

发表于 2020-08-15 分类于探索

前言

transform本质上就是一个仿射变换（即线性变换 + 平移），从CSS给定的transform-function可以看出，内置的函数将变换分为了2D变换和3D变换两种，但是从CSS规范来看，2D变换函数也只不过是3D变换函数的特殊形式而已，所以transform属性从原理上来说就是一个3D仿射变换函数。

关于仿射变换的详细数学解释，可以参考：
如何通俗地讲解「仿射变换」这个概念？ - 马同学的回答 - 知乎
https://www.zhihu.com/question/20666664/answer/157400568

仿射变换的核心就是变换矩阵了，因此transform属性的两个核心函数就是matrix()和matrix3d()；

matrix()函数

仿射变换通常是通过齐次坐标进行变换的，因此2D变换矩阵也就相应地变成了3x3的齐次矩阵：

\begin{bmatrix} a & c & t_{x} \\ b & d & t_{y} \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

上面就是matrix()函数的一般数学形式了，其中 $a, b, c, d, t_{x}, t_{y}$ 就是该函数的六个参数了；属于2D变换的transform-function有：

translate/translateX/translateY
scale/scaleX/scaleY
rotate
skew/skewX/skewY

也就是说上面这些变换函数完全可以通过matrix()函数进行等价替换；这里做了一个Demo来体现matrix()函数与这些变换函数等价的体现；

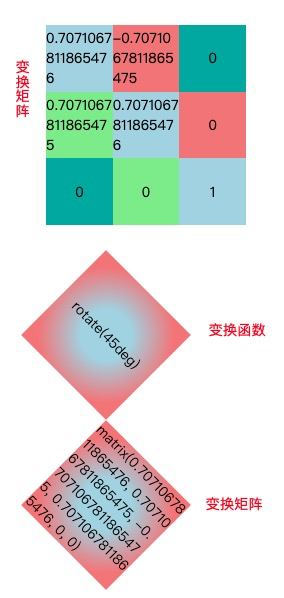
每种仿射变换之间的形式还是有所区别的，有必要弄清楚每种变换对应矩阵形式（之前就是对斜切变换的矩阵一直有误解……）：

\begin{aligned} M_{平移} &= \begin{bmatrix} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{bmatrix} \\[4ex] M_{缩放} &= \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \\[4ex] M_{旋转} &= \begin{bmatrix} cos\alpha & -sin\alpha & 0 \\ sin\alpha & cos\alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \\[4ex] M_{斜切} &= \begin{bmatrix} 1 & tan\alpha & 0 \\ tan\beta & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}

matrix3d()函数

同理，matrix3d()就是3D变换矩阵了，对应的就是4x4齐次矩阵：

\begin{bmatrix} a_1 & a_2 & a_3 & a_4 \\ b_1 & b_2 & b_3 & b_4 \\ c_1 & c_2 & c_3 & c_4 \\ d_1 & d_2 & d_3 & d_4 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

因此，matrix3d()函数就有16个参数，需要注意参数的顺序是列主导的，也就是：

matrix3d(a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, d3, a4, b4, c4, d4)

为何这里不省略一些矩阵元素，像matrix()那样呢？大概是matrix3d除了模拟仿射变换，还要提供透视投影变换，因此需要完整的矩阵元素；属于3D变换的transform-function有：

translateZ
scaleZ
rotateX/rotateY/rotateZ/rotate3d
perspective

也就是说上面的变换函数都可以使用matrix3d()函数进行等价替换；平移和缩放的3D变换矩阵形式同2D形式无本质差异，就是相应的扩展了一个维度而已，值得关注的是绕任意轴进行旋转及透视投影相关的变换矩阵；

rotate3d()函数

rotate3d()函数实际上就是一个绕任意轴进行旋转的变换，它接受旋转轴的方向及旋转角度；

rotate3d(x, y, z, α)

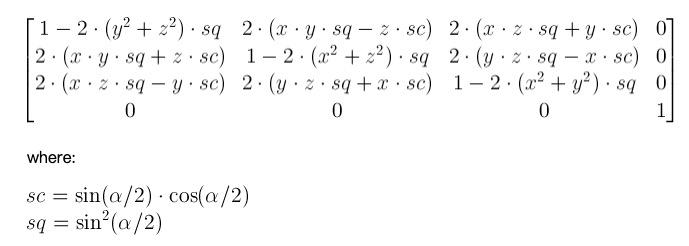
上面就是对应的3D旋转变换矩阵，其中 $(x, y, z)$ 就是旋转轴的方向， $\alpha$ 为旋转角度；

perspective()函数

该变换函数的作用就是设置当前视点距离屏幕（z = 0）平面的距离，从而形成相应的透视投影效果；

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & -\large{\frac{1}{d}} & 1 \end{bmatrix}

前言

matrix()函数

matrix3d()函数

rotate3d()函数

perspective()函数

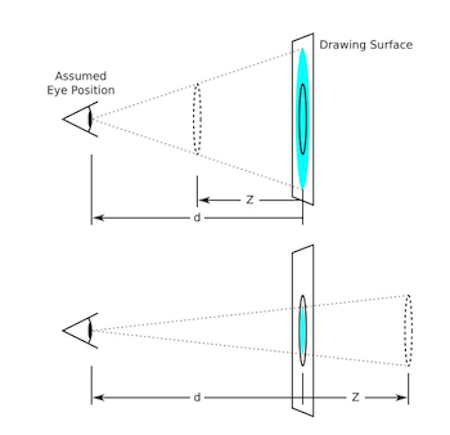
相关文档